引言
交叉熵主要是用来刻画实际输出和期望输出的接近程度。比如做分类任务训练时,输出数据类别和样本标注的类别之间是有差异的,通过交叉熵的方式可来刻画这种差异。
信息量
信息量是指信息多少的度量。度量信息量的基本单位是比特,如果信源是等概率出现时,使用哈特莱信息定量化公式即可计算出来。
\[I=log_2(m)\]m表示信源符号种类数。
实际情况往往是不确定的,香农指出信源给出的符号是随机的,信源的信息量应是概率的函数,以信源的信息熵表示。
\[H(U)=-\sum_{i=1}^N p_i{log_2(p_i)}\]\(p_i\)表示信源不同种类符号的概率。
若信源被等概率量化为4种符号,这个信源每个符号所给出的信息量应为:
\[\begin{align*} & I=log_2(4)=2bit\\ & H(U)=-\sum_{i=1}^4 \frac{1}{4} log_2(\frac{1}{4})=2bit \end{align*}\]从公式可以看出哈莱特信息定量就是香农信息熵在等概率下的特例。
信息熵
信息熵是解决对信息的量化度量,用来描述信源的不确定度。这里的熵是借用了热力学中热熵表示分子状态混乱程度的物理量,用到信息度量上表示信息中排除了冗余后的平均信息量。
通常一个信源发出什么符号是不确定的,衡量它可以根据其出现的概率来度量。概率大表示出现机会多,那么不确定性小;概率小表示出现机会少,那么不确定性大。不确定函数F是概率P的减函数,两个独立符号所产生的不确定性应等于各自不确定性之和,即为:
\[F(P1,P2)=F(P1)+F(P2)\]这称为可加性。同时满足这两个条件的函数F是对数函数:
\[F(P)=log2(1/p)=-log2(p)\]在信源中,考虑的不是单个符号发生的不确定性,而是要考虑这个信源所有可能发生情况的平均不确定性。那么信源的平均不确定性应该为当个符号不确定性的统计平均值(即期望E),可称为信息熵,即为下图公式:
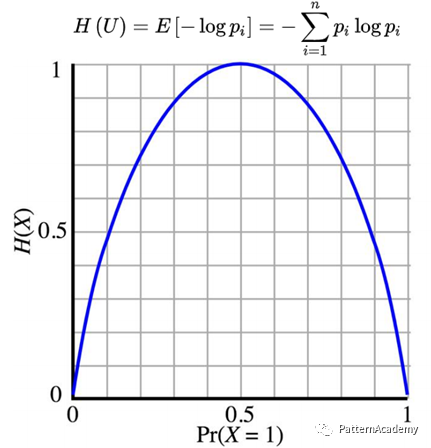
举例最简单的单符号信源仅取0和1两个元素,即二元信源,其概率为P和Q=1-P,该信源的熵为上图所示,离散信源的信息熵具有如下性质:
- 非负性:即收到一个信源符号所获得的信息量应为正值,H(U)≥0
- 对称性:即对称于P=0.5
- 确定性:H(1,0)=0,即P=0或P=1已是确定状态,所得信息量为零
- 极值性:因H(U)是P的上凸函数,且一阶导数在P=0.5时等于0,所以当P=0.5时,H(U)最大。
注:想到那个小鼠试毒药问题是利用信息熵理解的思路来解决的一个小问题。
交叉熵
在信息论中,交叉熵是表示两个概率分布p和q,其中p表示真实分布,q表示非真实分布,在相同的一组事件中,用非真实分布q来表示某个事件发生所需要的平均比特数。假设现在有一个样本集中两个概率分布p和q,其中p为真实分布,q为非真实分布。
按照真实分布p来衡量识别一个样本所需编码长度的期望为:
\[H(p)=\sum_{i} p(i)log_2(\frac{1}{p(i)})\]如果采用错误的分布q来表示来自真实分布p的平均编码长度,则应该是:
\[H(p,q)=\sum_{i=1} p(i)log_2(\frac{1}{q(i)} )\]H(p,q)称之为交叉熵。
假设期望N=2输出p=(0.9,0.1),实际输出\(q_1\)=(0.6,0.4),\(q_2\)=(0.8,0.2),那么:
\[\begin{align*} & H(p,q_1)=-[0.9*log_2(0.6)+0.1*log_2(0.4)]=0.79\\ & H(p,q_2)=-[0.9*log_2(0.8)+0.1*log_2(0.2)]=0.42 \end{align*}\]import numpy as np
def cross_entropy(p, q):
p = np.float_(p)
q = np.float_(q)
return -sum([p[i]*np.log2(q[i]) for i in range(len(p))])
p = np.array([0.9, 0.1])
q1 = np.array([0.6, 0.4])
q2 = np.array([0.8, 0.2])
print(cross_entropy(p, q1)) # ≈0.79
print(cross_entropy(p, q2)) # ≈0.42
print(cross_entropy(q2, p)) # ≈1.45,交叉熵是非对称的
交叉熵是可通过KL散度推导出来:
\[\begin{align*} H(P,Q) &= H(P) + D_KL(P||Q)\\ &= -E_{x~P}logQ(x) \\ &= -\sum_{x}{P(x)logQ(x)} \end{align*}\]由于H(P)与Q无关,所以最小化Q与P之间的交叉熵就等价于最小化KL散度。
交叉熵损失
交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数。
二分类的交叉熵损失
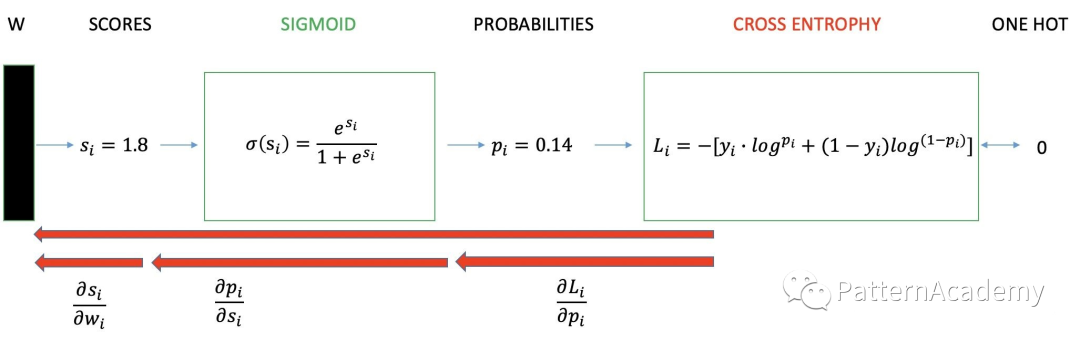
多分类的交叉熵损失
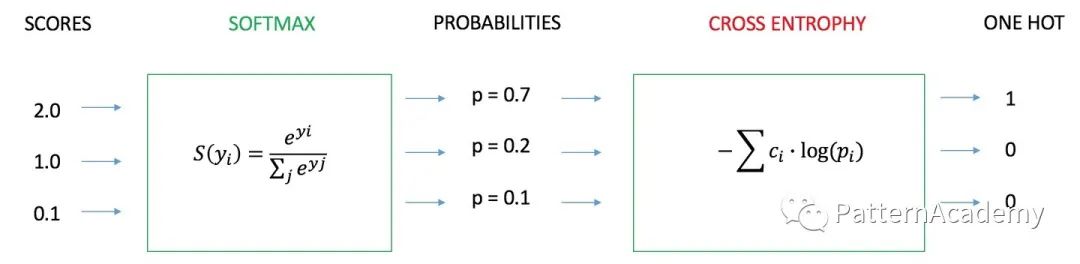
注:两图来源于知乎
交叉熵可以在神经网络(机器学习)中作为损失函数,P表示真实标记的分布,Q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量P与Q的相似性。交叉熵作为损失函数还有一个好处是使用 Sigmoid 函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
Pytorch 中的交叉熵损失
交叉熵损失函数经常用于分类问题中,特别是在神经网络做分类问题时,也经常使用交叉熵作为损失函数。Pytorch 中的 CrossEntropyLoss 类来实现交叉熵损失计算,通过整合 LogSoftmax 和 NLLLoss 来实现过程如下:
import torch
input=torch.randn(3,3)
target=torch.tensor([0,2,1])
# 下面两步可以直接使用lsm=torch.nn.LogSoftmax(dim=1)来代替
sm=torch.nn.Softmax(dim=1)
input=torch.log(sm(input))
loss=torch.nn.NLLLoss()
loss(input,target)
# 上面整体的过程和下面代码功能一致
loss=torch.nn.CrossEntropyLoss()
loss(input,target)
NLLLoss 是 Negative Log Likelihood Loss 的简写,翻译为 “负对数似然损失函数”,但并不计算对数,只是利用对数运算后的值(故需要和 LogSofmax 组合),进一步结合真实标签计算“负对数似然值”。
\[nllloss=-\sum_{n=1}^N{y_n logprob(x_n)}\]“似然”的含义为:所求概率分布与真实概率分布的相似程度。在分类任务中,“似然”的含义就是预测值与真实标签(one-hot 类型)的接近程度。“负”的解释:“似然”值越大越好(即越接近真实),取负值就变为“越小越好”(这正是损失函数 Loss 的特点),就可用梯度下降法了。
# 1.Examples::
input = torch.randn((3, 2), requires_grad=True)
target = torch.rand((3, 2), requires_grad=False)
loss = F.binary_cross_entropy(F.sigmoid(input), target)
loss.backward()
# 2.Examples::
input = torch.randn(3, 5, requires_grad=True)
target = torch.randint(5, (3,), dtype=torch.int64)
loss = F.cross_entropy(input, target)
loss.backward()
# 3.Example::
# input is of size N x C = 3 x 5
input = torch.randn(3, 5, requires_grad=True)
# each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 4])
output = F.nll_loss(F.log_softmax(input), target)
output.backward()