GaphSAGE：一种节点表示学习方法

引言

在对图节点进行表示学习中，一般方法本质上是 Transductive【直推式】，不能自然地泛化到未见过的节点。本文介绍的 GraphSAGE 是一个 Inductive【归纳式】的框架，通过从一个节点的局部邻居采样并聚合节点特征，即利用节点特征信息（比如文本属性）来高效地为未见过的节点生成 Embedding。

基本思路

GraphSAGE 不是试图学习一个图上所有节点的 Embedding，而是学习一个为每个节点产生 Embedding 的映射，学习一个节点的信息是如何通过其邻居节点的特征聚合而来，学习到了这样的”聚合函数“。该方法学到的节点 Embedding 是根据节点邻居关系的变化而变化，如果旧节点建立了一些新的边，其对应的 Embedding 也会进行相应变化。

流程

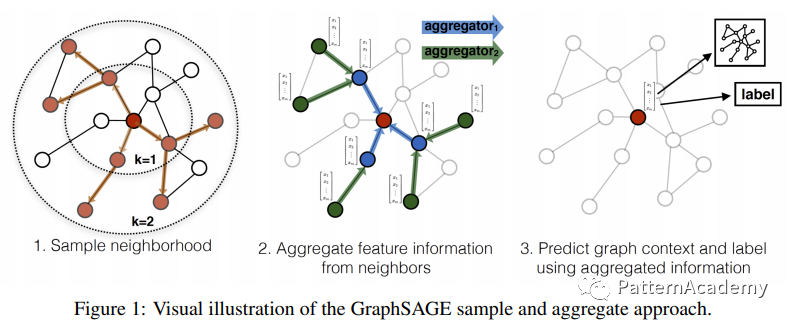
GraphSAGE是Graph SAmple and aggreGatE 的缩写，从名称上也看出了该方法的大致过程：

对目标节点的邻居进行采样（采样为固定数量，如果不足就采取有放回的采样；
根据选择的聚合函数聚合邻居节点蕴含的信息；
得到目标节点的向量表示后进行下游任务（比如：分类任务）

架构图

算法

GraphSAGE 的前向传播描述了如何使用聚合函数对节点的邻居信息进行聚合，从而生成节点 Embedding ，算法如下：

设置网络的层数K，也代表着每个节点能够聚合的邻接点的跳数
循环处理每个节点V，把节点的特征向量作为输入
聚合k−1层（可以理解为比当前层更外一层）中节点v的邻居节点u的 Embedding
k层节点v的特征表示为k-1层节点v特征和上步聚合邻居节点的特征进行合并（求和）
每一层操作完后进行归一化操作

算法1

使用 Minibatch 方式伪代码如下：

算法2

使用 DGL 框架的一个代码示例：

# 通过sampler来完成邻居几跳和个数采样，设置为第一跳25，第二跳10
sampler = dgl.dataloading.MultiLayerNeighborSampler([10,25])
dataloader = dgl.dataloading.NodeDataLoader(G,
                                    ids,
                                    sampler,
                                    batch_size=5000,
                                    shuffle=False,
                                    drop_last=False,
                                    num_workers=4)
                                    
# 通过dataloader来按照节点批次处理，下面为每次10000个节点，并获取它的二跳子图（blocks）
for step, (input_nodes, output_nodes, blocks) in enumerate(dataloader):
    # [Block(num_src_nodes=30840, num_dst_nodes=13708, num_edges=37639), Block(num_src_nodes=13708, num_dst_nodes=10000, num_edges=3886)]
    blocks = [block.int().to(device) for block in blocks]
    batch_inputs = nfeat[input_nodes].to(1)
    # tensor([   0,    1,    2,  ..., 9997, 9998, 9999])
    print(output_nodes)
 
# 定义SAGE模型，可以定义多层网络                           
class SAGE(nn.Module):
    def init(self, in_feats, n_hidden, n_classes, n_layers, activation, dropout):
        self.layers = nn.ModuleList()
        if n_layers > 1:
            self.layers.append(dglnn.SAGEConv(in_feats, n_hidden, 'mean'))
            for i in range(1, n_layers - 1):
                self.layers.append(dglnn.SAGEConv(n_hidden, n_hidden, 'mean'))
            self.layers.append(dglnn.SAGEConv(n_hidden, n_classes, 'mean'))
        else:
            self.layers.append(dglnn.SAGEConv(in_feats, n_classes, 'mean'))
        self.dropout = nn.Dropout(dropout)
        self.activation = activation

    def forward(self, blocks, x):
        h = x
        for l, (layer, block) in enumerate(zip(self.layers, blocks)):
            # 把最外层的邻居集合和节点特征输入到SAGEConv完成聚合
            # SAGEConv具体操作为：
                # graph.update_all(msg_fn, fn.mean('m', 'neigh'))
                # h_neigh = graph.dstdata['neigh']                
                # rst = self.fc_self(h_self) + h_neigh
                # rst = self.activation(rst)   # activation
                # rst = self.norm(rst) # normalization
            # 由外到内迭代，外层的输出作为内层的输入            
            h = layer(block, h)
            if l != len(self.layers) - 1:
                # 最后一层不用进行激活操作了，输出直接就可以作为节点表示
                h = self.activation(h)
                h = self.dropout(h)
        return h

聚合函数

GraphSAGE 提供了四种聚合邻居节点的函数：

Mean aggregator：对节点v邻居节点的特征向量求均值

\[\mathbf{h}_{v}^{k} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{v}^{k-1}\right\} \cup\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}\right)\right.\]

GCN aggregator：对节点使用卷积方式聚合（具体参见 GCN 论文）

\[\begin{align*} \text { aggregate }\left(X_{i}\right) &=\hat{D}^{-0.5} \hat{A} \hat{D}^{-0.5} X \\ &=\sum_{k=1}^{N} \hat{D}_{i k}^{-0.5} \sum_{j=1}^{N} \hat{A}_{i j} X_{j} \sum_{l=1}^{N} \hat{D}_{i l}^{-0.5} \\ &=\sum_{j=1}^{N} \hat{D}_{i i}^{-0.5} \hat{A}_{i j} X_{j} \hat{D}_{j j}^{-0.5} \\ &=\sum_{j=1}^{N} \frac{1}{\hat{D}_{i i}{ }^{0.5}} \hat{A}_{i j} \frac{1}{\hat{D}_{j j}{ }^{0.5}} X_{j} \\ &=\sum_{j=1}^{N} \frac{\hat{A}_{i j}}{\sqrt{\hat{D} i i \hat{D} j j}} X_{j} \end{align*}\]

Pooling aggregator：首先对目标节点的邻居节点的Embedding向量进行一次非线性变换，然后进行一次Pooling操作(max pooling or mean pooling)

\[AGGREGATE_{k}^{\text {pool }}=\max \left(\left\{\sigma\left(\mathbf{W}_{\text {pool }} \mathbf{h}_{u_{i}}^{k}+\mathbf{b}\right), \forall u_{i} \in \mathcal{N}(v)\right\}\right)\]

LSTM aggregator：使用LSTM来增强表达能力，因为LSTM模型涉及到节点排序，所以在使用时需要对节点进行排序处理后才能输入LSTM模型

使用 DGL 框架的一个代码示例：

if self._aggre_type == 'mean':
    graph.srcdata['h'] = self.fc_neigh(feat_src) if lin_before_mp else feat_src
    # 使用平均算子对邻居节点特征进行操作
    graph.update_all(msg_fn, fn.mean('m', 'neigh'))
    h_neigh = graph.dstdata['neigh']
elif self._aggre_type == 'gcn':
    check_eq_shape(feat)
    graph.srcdata['h'] = self.fc_neigh(feat_src) if lin_before_mp else feat_src
    if isinstance(feat, tuple):  # heterogeneous，可以处理二分图
        graph.dstdata['h'] = self.fc_neigh(feat_dst) if lin_before_mp else feat_dst
    else:
        if graph.is_block:
            graph.dstdata['h'] = graph.srcdata['h'][:graph.num_dst_nodes()]
        else:
            graph.dstdata['h'] = graph.srcdata['h']
    graph.update_all(msg_fn, fn.sum('m', 'neigh'))  # 对邻居节点特征求和
    # divide in_degrees，除以入度操作
    degs = graph.in_degrees().to(feat_dst)
    h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
elif self._aggre_type == 'pool':
    # 添加了一个pool层，做非线性变换
    graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
    # 使用max操作
    graph.update_all(msg_fn, fn.max('m', 'neigh'))
    h_neigh = self.fc_neigh(graph.dstdata['neigh'])
elif self._aggre_type == 'lstm':
    graph.srcdata['h'] = feat_src
    # 做LSTM操作
    graph.update_all(msg_fn, self._lstm_reducer)
    h_neigh = self.fc_neigh(graph.dstdata['neigh'])

参数学习

GraphSAGE 是可以使用有监督学习和无监督学习两种方式：

有监督学习：监督学习形式根据任务的不同可以直接设置目标函数即可，如最常用的节点分类任务使用交叉熵损失函数

使用 DGL 框架的一个代码示例：

for epoch in range(args.n_epochs):
    model.train()
    if epoch >= 3:
        t0 = time.time()
    # forward
    logits = model(g, features)
    # 直接使用交叉熵损失即可
    loss = F.cross_entropy(logits[train_nid], labels[train_nid])
  
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

无监督学习：采用负采样的方法，然后通过比较相邻节点相似度高于非相邻节点相似度

\[J \mathcal{G}\left(\mathbf{z}_{u}\right)=-\log \left(\sigma\left(\mathbf{z}_{u}^{T} \mathbf{z}_{v}\right)\right)-Q \cdot \mathbb{E}_{v_{n} \sim P_{n}(v)} \log \left(\sigma\left(-\mathbf{z}_{u}^{T} \mathbf{z}_{v_{n}}\right)\right)\]

说明：

节点v是节点u的“邻居”
Pn是负采样的概率分布
Q是负采样的个数
通过点积来计算节点相似度

使用 DGL 框架的一个代码示例：

# 负采样方法，根据与节点的度的幂成正比的概率分布对负样本目标节点进行采样
class NegativeSampler(object):
    def __init__(self, g, k, neg_share=False):
        self.weights = g.in_degrees().float() ** 0.75  # 缓存概率分布
        self.k = k   # 采样个数
        self.neg_share = neg_share  # 是否共享负采样node到不同Positive节点中

    def __call__(self, g, eids):
        src, _ = g.find_edges(eids)
        n = len(src)
        if self.neg_share and n % self.k == 0:
            dst = self.weights.multinomial(n, replacement=True)
            dst = dst.view(-1, 1, self.k).expand(-1, self.k, -1).flatten()
        else:
            dst = self.weights.multinomial(n*self.k, replacement=True)
        src = src.repeat_interleave(self.k)  # 重复交错
        return src, dst
        
# 无监督方法定义的损失函数
class CrossEntropyLoss(nn.Module):
    def forward(self, block_outputs, pos_graph, neg_graph):
        with pos_graph.local_scope():
            pos_graph.ndata['h'] = block_outputs
            # 使用点积来计算两节点相似度，这里Postive中认为邻居节点相似度高
            pos_graph.apply_edges(fn.u_dot_v('h', 'h', 'score'))
            pos_score = pos_graph.edata['score']
        with neg_graph.local_scope():
            neg_graph.ndata['h'] = block_outputs
            # 这里Negative中认为非邻居节点相似度低
            neg_graph.apply_edges(fn.u_dot_v('h', 'h', 'score'))
            neg_score = neg_graph.edata['score']

        score = th.cat([pos_score, neg_score])
        label = th.cat([th.ones_like(pos_score), th.zeros_like(neg_score)]).long()
        # 通过二分类的交叉熵损失
        loss = F.binary_cross_entropy_with_logits(score, label.float())
        return loss

引用

[1] Open Graph Benchmark

[2] DGL 官网

[3] GraphSAGE 论文