引言
GCN是一种图卷积神经网络,利用离散化卷积运算来完成节点邻居特征表示节点特征的图表示学习方法。
卷积
在泛函分析中,卷积(Convolution)是通过两个函数f和g生成第三个函数的一种数学算子,表征函数f与g经过翻转和平移的重叠部分函数值乘积对重叠长度的积分。 卷积的“卷”,指函数的翻转,从 g(x) 变成 g(-x) 的这个过程,同时“卷”还有滑动的意味。卷积的“积”,指的是积分或加权求和。 简单定义为f(x),g(x)是R上的两个可积函数,作积分:
\[\int_{- \infty}^\infty f\left(t\right)g\left(x-t\right)dt\]这样,随着x的不同取值,这个积分就定义了一个新函数h(x),称为函数f(x)与g(x)的卷积,记为:
\[h \left(x\right)=\left(f·g \right)\left(x\right)\]卷积的概念可以扩展到数列上,如果上述f和g是序列则卷积定义为:
\[h \left(x\right)=\sum_{i=- \infty}^{\infty}f\left(i\right)g\left(x-i\right)\]摘自沈华伟老师PPT:

由卷积得到的函数h一般要比f和g都光滑。特别当g为具有紧致集的光滑函数,f为局部可积时,它们的卷积f·g也是光滑函数。卷出发点是施加一种约束和平滑,积是一种参照”全局”的叠加。
卷积定理指出,函数卷积的傅里叶变换是函数傅里叶变换的乘积。即一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积:
\[\mathcal{F}\left[g\left(x\right)\right]=\mathcal{F}\left[f\left(x\right)\right] \mathcal{F}\left[g\left(x\right)\right]\]CNN 中的卷积
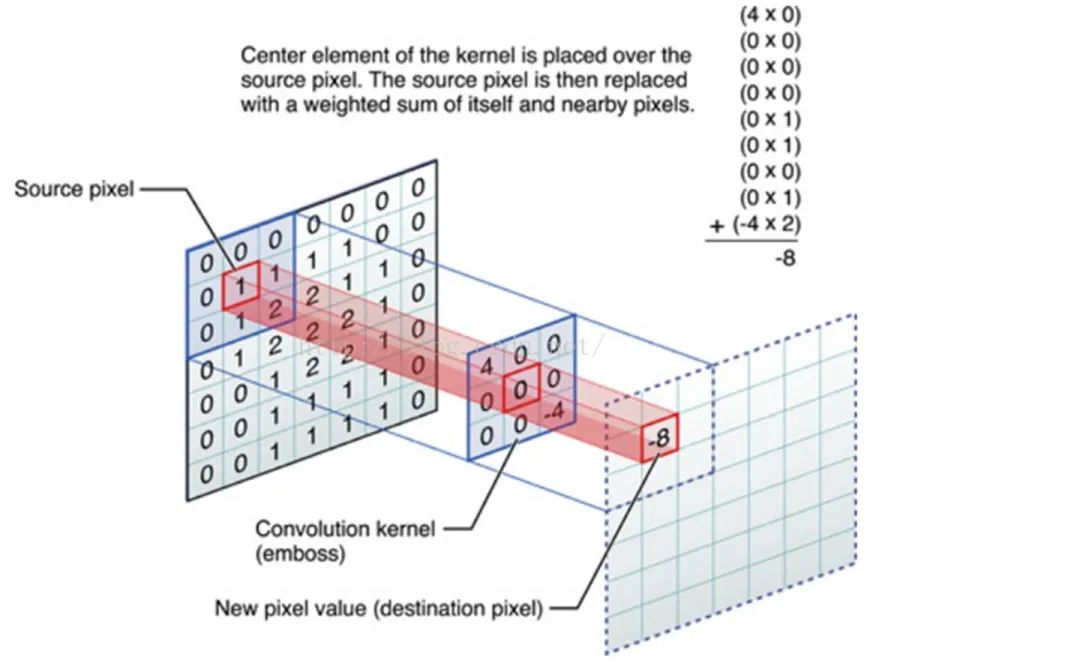
CNN 中的卷积是利用一个共享参数的过滤器也就是卷积核,通过计算中心像素点以及相邻像素点的加权和来实现空间特征的提取。卷积核的权重系数就是要学习的参数。
传统的卷积神经网络只能处理欧氏空间数据具有平移不变性,平移不变性使得我们可以在输入数据空间定义全局共享的卷积核,从而定义卷积神经网络。以图像数据为例,一张图片可以表示为欧氏空间中一组规则散布的像素点,平移不变性则表示任意像素点为中心,可以获取相同尺寸的局部结构。基于此,卷积神经网络通过学习在每个像素点共享的卷积核来建模局部连接,进而为图片学习到意义丰富的隐层表示。
Graph 卷积难点
图像做卷积是因为是在欧氏空间,Graph 的结构是非欧空间,不能使用欧氏空间中 CNN 一样的离散卷积,因为在 Graph 数据上无法保持平移不变性形。可以理解为:图像邻域是一个规则的矩阵,Graph 的邻域是不规则的关系(每个节点周围邻居数是不固定的,也就是每个节点的局部结构各异)。
那么针对 Graph 卷积的难点出发有两类方法,其实是一类方法(Spectral 方法是 Spatial 方法的一个特例),下面详细说明:
1、Spectral 方法
Spectral 方法即谱方法,主要过程是通过把节点域的卷积转换到谱域上完成卷积后再反向转换回节点域。也就是把卷积定义在谱域上,节点域和谱域的转换使用傅里叶变换和逆变换实现。这样做的原因是谱域上卷积可以克服欧式距离的问题,这类方法也存在一个问题就是在谱域定义的卷积核在节点域不是局部化的(容易出现级联)。
定义一个图:包括邻接矩阵和节点特征

图拉普拉斯矩阵:定义拉普拉斯算子并作归一化处理
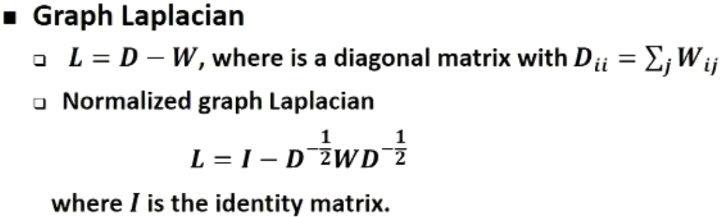
上述 Normalized 方法是 Symmetric normalized Laplacian(用在 GCN 等模型上,数学性质要好:满足对称性)
\[L^{sys}=D^{-\frac{1}{2}} L D^{-\frac{1}{2}}\]另一种方法是 Random walk normalized Laplacian(用在随机行走、PageRank 中)
\[L^{rw}=D^{-1} L\]拉普拉斯矩阵的谱分解:谱分解就是特征分解也是对角化处理,特征分解的充要条件是n阶方阵存在n个线性无关的特征向量。拉普拉斯矩阵是半正定对称矩阵,这里处理的都是实数就是实对称矩阵,实对称矩阵的特征向量总能做一个施密特正交化处理(实对称矩阵性质),得到的是一组 Orthonormal eigenvectors(标准正交的特征向量)。

图上的傅里叶基:傅里叶变换是指在时域上的信号变成频域上的信号,这其中关键是傅里叶基,时域上的变换,基是一系列正弦波。图上的傅里叶变换是把时域上的信号改为图节点上的信号,这里基定义为拉普拉斯矩阵的所有特征向量,这个基对应的频率为特征值,也就是特征值越大说明它所代表的特征向量对应的信号是一个高频信号。如何理解特征值对应的频率,拉普拉斯矩阵有一个特殊的特征值0和对应全1特征向量x,Lx=0x,说明频率为0时特征向量就是平的(都是1)。

图上的傅里叶变换和逆变换:以U做基,把节点域的信号转换到一个新的空间(谱域)表示。公式中x和每一个基点积后的值,刻画了x每个信号分解在正交基上的每一个坐标值(因为是正交的所以直接可以通过点积来算出各坐标轴上的投影)。所以x^就已经刻画了原来信号在U这些基代表的空间中的新的表示,也就是进入到谱域,表示每一个基的权重(把每个信号分解到这个里面了)。

卷积理论:两个信号卷积是它们傅里叶变换后的点积

图上的卷积定义:基于卷积理论图上的卷积是在谱域中定义的,即给定信号x和信号y先做傅里叶变换后再做点积,最后通过傅里叶逆变换到原空间,其中卷积核为
\[U^T y\]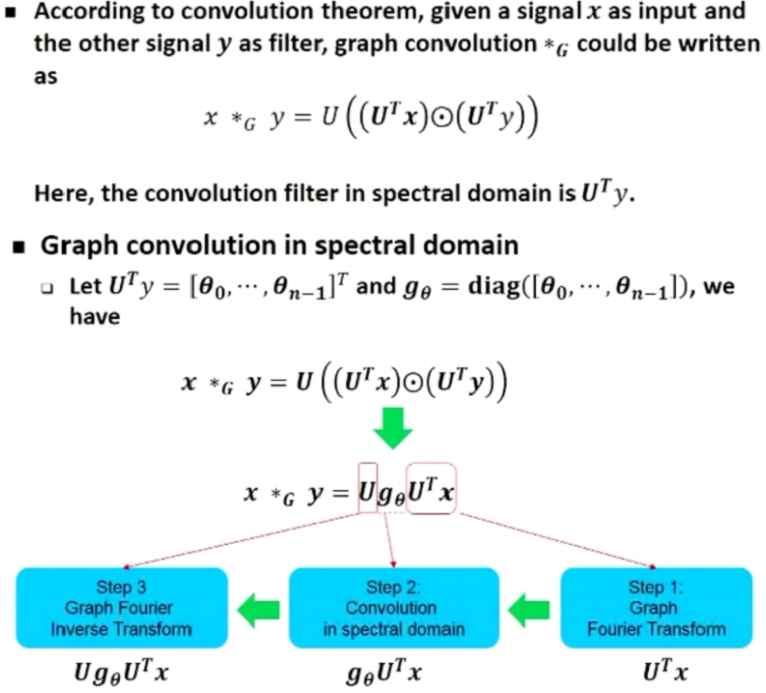
上述过程是对卷积核做了变形处理更方便理解为卷积运算。
谱方法核心是定义了上述的图卷积过程但在实际应用中存在如下问题:需要计算拉普拉斯矩阵、傅里叶变换运算的高复杂度、非Localized。
ChebyNet 提出:为了解决谱方法的问题,通过多项式函数(以拉普拉斯矩阵分解的对角阵作为基)来近似原gθ,原公式U消去了。这就带来三个优点:特征分解不用做了,因为U不用了;计算复杂度降低了,因为拉普拉斯矩阵和边多少有关和节点平方无关;可以控制 Localized 了,比如k为1是就表示x和一阶邻居相乘。

2、Spatial 方法
Spatial 方法即空间方法,直接在节点域定义卷积,通过邻居节点特征来表示,难点是节点的邻域大小不一样。
卷积过程分解:分解图卷积过程,通过类比的方法找到改造的步骤,Graph中难点是确定邻域(邻居的多少不固定,不能去参数共享)。
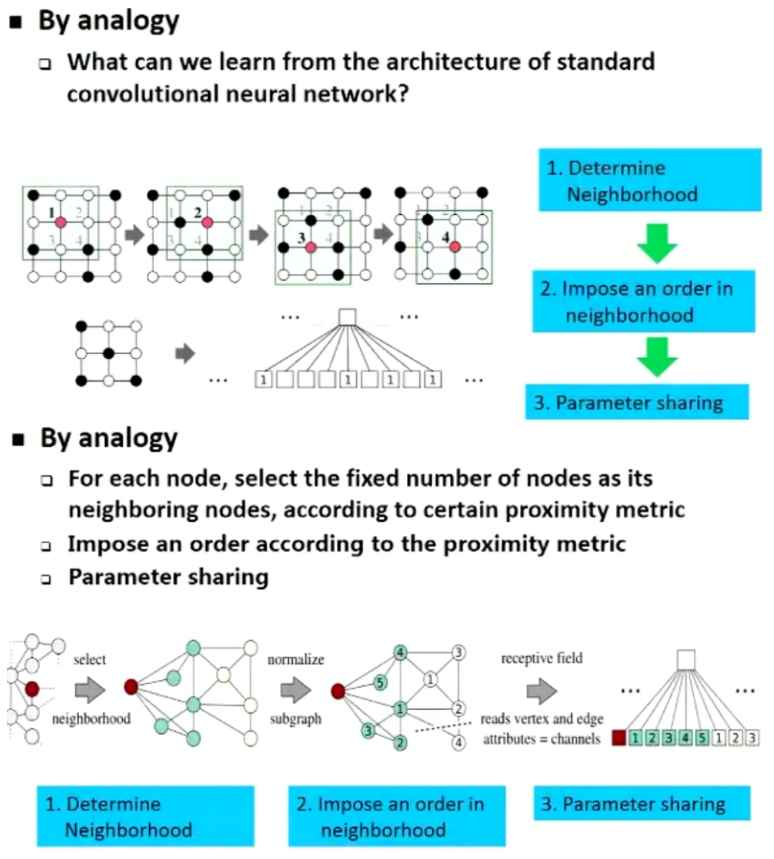
基于相似度量找固定邻居数:通过确定相似度量方法找最近的k个邻居作为邻域,序按照相似度大小确定。
卷积改造成采样-聚合:通过对邻居的采样得到k个邻居,序不再需要,改成聚合函数来去掉序的依赖,代表方法 GraphSAGE
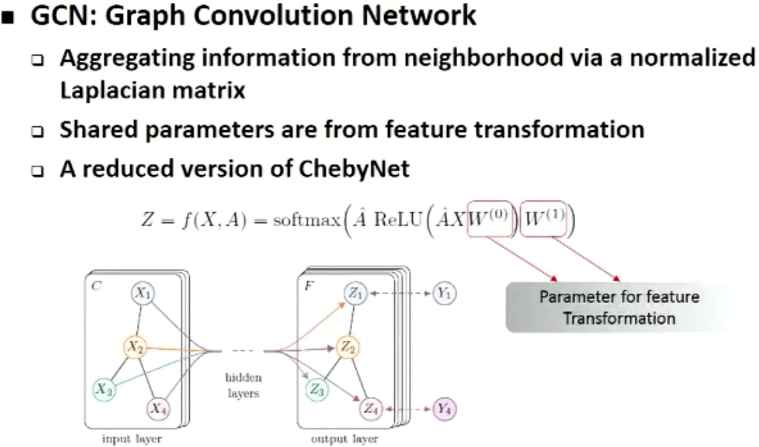
GCN 提出:主要思想是通过邻居来表示自己,XW表示对原节点特征做特征变换,然后用邻接矩阵A做聚合。整体是通过A做硬编码卷积没有像 CNN 中卷积核作为参数。

摘自 DGL 框架中的代码:
### GCN convolution along the graph structure
class GraphConv(nn.Module):
def __init__(self,
in_feats,
out_feats,
norm='both',
weight=True,
bias=True,
activation=None,
allow_zero_in_degree=False):
super(GraphConv, self).__init__()
if norm not in ('none', 'both', 'right', 'left'):
raise DGLError('Invalid norm value. Must be either "none", "both", "right" or "left".'
' But got "{}".'.format(norm))
self._in_feats = in_feats
self._out_feats = out_feats
self._norm = norm
self._allow_zero_in_degree = allow_zero_in_degree
if weight:
self.weight = nn.Parameter(th.Tensor(in_feats, out_feats))
else:
self.register_parameter('weight', None)
if bias:
self.bias = nn.Parameter(th.Tensor(out_feats))
else:
self.register_parameter('bias', None)
self._activation = activation
def forward(self, graph, feat, weight=None, edge_weight=None):
with graph.local_scope():
if not self._allow_zero_in_degree:
if (graph.in_degrees() == 0).any():
raise DGLError('There are 0-in-degree nodes in the graph.')
aggregate_fn = fn.copy_src('h', 'm')
if edge_weight is not None: # 如果有边权重定义聚合函数要用节点*边权重
assert edge_weight.shape[0] == graph.number_of_edges()
graph.edata['_edge_weight'] = edge_weight
aggregate_fn = fn.u_mul_e('h', '_edge_weight', 'm')
# (BarclayII) For RGCN on heterogeneous graphs we need to support GCN on bipartite.
feat_src, feat_dst = expand_as_pair(feat, graph)
if self._norm in ['left', 'both']:
degs = graph.out_degrees().float().clamp(min=1)
if self._norm == 'both':
norm = th.pow(degs, -0.5)
else:
norm = 1.0 / degs
shp = norm.shape + (1,) * (feat_src.dim() - 1)
norm = th.reshape(norm, shp)
feat_src = feat_src * norm
if weight is not None:
if self.weight is not None:
raise DGLError('External weight is provided while.')
else:
weight = self.weight
if self._in_feats > self._out_feats:
# mult W first to reduce the feature size for aggregation.
if weight is not None:
feat_src = th.matmul(feat_src, weight)
graph.srcdata['h'] = feat_src
# 可以看到节点的特征变成了其邻居的特征之和
graph.update_all(aggregate_fn, fn.sum(msg='m', out='h'))
rst = graph.dstdata['h']
else:
# aggregate first then mult W
graph.srcdata['h'] = feat_src
# 可以看到节点的特征变成了其邻居的特征之和
graph.update_all(aggregate_fn, fn.sum(msg='m', out='h'))
rst = graph.dstdata['h']
if weight is not None:
rst = th.matmul(rst, weight)
if self._norm in ['right', 'both']:
degs = graph.in_degrees().float().clamp(min=1)
if self._norm == 'both':
norm = th.pow(degs, -0.5)
else:
norm = 1.0 / degs
shp = norm.shape + (1,) * (feat_dst.dim() - 1)
norm = th.reshape(norm, shp)
rst = rst * norm
if self.bias is not None:
rst = rst + self.bias
if self._activation is not None:
rst = self._activation(rst)
return rst
GAT 提出:针对 GCN 的缺点来参数化卷积核,通过学习参数来实现真正意义上的卷积核,主要思路是通过了 Attention 的机制来参数化卷积核,W表示特征变换的参数,a表示卷积核参数。

摘自 DGL 框架中的代码:
class GATConv(nn.Module):
def __init__(self,
in_feats,
out_feats,
num_heads,
feat_drop=0.,
attn_drop=0.,
negative_slope=0.2,
residual=False,
activation=None,
allow_zero_in_degree=False,
bias=True):
super(GATConv, self).__init__()
self._num_heads = num_heads
self._in_src_feats, self._in_dst_feats = expand_as_pair(in_feats)
self._out_feats = out_feats
self._allow_zero_in_degree = allow_zero_in_degree
if isinstance(in_feats, tuple):
self.fc_src = nn.Linear(
self._in_src_feats, out_feats * num_heads, bias=False)
self.fc_dst = nn.Linear(
self._in_dst_feats, out_feats * num_heads, bias=False)
else:
self.fc = nn.Linear(
self._in_src_feats, out_feats * num_heads, bias=False)
self.attn_l = nn.Parameter(th.FloatTensor(size=(1, num_heads, out_feats)))
self.attn_r = nn.Parameter(th.FloatTensor(size=(1, num_heads, out_feats)))
self.feat_drop = nn.Dropout(feat_drop)
self.attn_drop = nn.Dropout(attn_drop)
self.leaky_relu = nn.LeakyReLU(negative_slope)
if bias:
self.bias = nn.Parameter(th.FloatTensor(size=(num_heads * out_feats,)))
else:
self.register_buffer('bias', None)
if residual:
if self._in_dst_feats != out_feats * num_heads:
self.res_fc = nn.Linear(
self._in_dst_feats, num_heads * out_feats, bias=False)
else:
self.res_fc = Identity()
else:
self.register_buffer('res_fc', None)
self.activation = activation
def forward(self, graph, feat, get_attention=False):
with graph.local_scope():
if not self._allow_zero_in_degree:
if (graph.in_degrees() == 0).any():
raise DGLError('There are 0-in-degree nodes in the graph.')
if isinstance(feat, tuple):
src_prefix_shape = feat[0].shape[:-1]
dst_prefix_shape = feat[1].shape[:-1]
h_src = self.feat_drop(feat[0])
h_dst = self.feat_drop(feat[1])
if not hasattr(self, 'fc_src'):
feat_src = self.fc(h_src).view(
*src_prefix_shape, self._num_heads, self._out_feats)
feat_dst = self.fc(h_dst).view(
*dst_prefix_shape, self._num_heads, self._out_feats)
else:
feat_src = self.fc_src(h_src).view(
*src_prefix_shape, self._num_heads, self._out_feats)
feat_dst = self.fc_dst(h_dst).view(
*dst_prefix_shape, self._num_heads, self._out_feats)
else:
src_prefix_shape = dst_prefix_shape = feat.shape[:-1]
h_src = h_dst = self.feat_drop(feat)
feat_src = feat_dst = self.fc(h_src).view(
*src_prefix_shape, self._num_heads, self._out_feats)
if graph.is_block:
feat_dst = feat_src[:graph.number_of_dst_nodes()]
h_dst = h_dst[:graph.number_of_dst_nodes()]
dst_prefix_shape = (graph.number_of_dst_nodes(),) + dst_prefix_shape[1:]
el = (feat_src * self.attn_l).sum(dim=-1).unsqueeze(-1)
er = (feat_dst * self.attn_r).sum(dim=-1).unsqueeze(-1)
graph.srcdata.update({'ft': feat_src, 'el': el})
graph.dstdata.update({'er': er})
# compute edge attention, el and er are a_l Wh_i and a_r Wh_j respectively.
graph.apply_edges(fn.u_add_v('el', 'er', 'e'))
e = self.leaky_relu(graph.edata.pop('e'))
# compute softmax
graph.edata['a'] = self.attn_drop(edge_softmax(graph, e))
# message passing
graph.update_all(fn.u_mul_e('ft', 'a', 'm'),
fn.sum('m', 'ft'))
rst = graph.dstdata['ft']
# residual
if self.res_fc is not None:
# Use -1 rather than self._num_heads to handle broadcasting
resval = self.res_fc(h_dst).view(*dst_prefix_shape, -1, self._out_feats)
rst = rst + resval
# bias
if self.bias is not None:
rst = rst + self.bias.view(
*((1,) * len(dst_prefix_shape)), self._num_heads, self._out_feats)
# activation
if self.activation:
rst = self.activation(rst)
if get_attention:
return rst, graph.edata['a']
else:
return rst
图的拉普拉斯矩阵
图的拉普拉斯矩阵,可以看作线性变换,起的作用与数学分析中的拉普拉斯算子是一样的。也就是说拉普拉斯矩阵就是图上的拉普拉斯算子,或者说是离散的拉普拉斯算子。拉普拉斯算子是沿着图上的边对信号求导(目的是刻画信号的平滑性)。
摘自知乎:


实对称矩阵
设A是n阶矩阵,若A的元素都是实数且满足
\[A=A^T\]则称矩阵A为n阶实对称矩阵。也就是全部是实数的对称矩阵。
摘自百度:

引用
[1] 知乎文章_深入理解卷积
[2] 沈华伟老师_图深度学习
[3] 知乎文章_拉普拉斯算子
[5] DGL 官网
[6] GraphSAGE 论文
[7] GCN 论文
[8] GAT 论文